EN MI BLOG VOY A PONER TEMAS MUY INTERESANTES SOBRE LAS TIC'S, LAS FINANZAS, AUDITORÌA INFORMATICA, SOFTWARE MOVIL, FINANZAS, Y MUCHO MAS Y TAL VEZ TESIS Y MONOGRAFÍAS, LIBROS, ETC.... OJO PARA TODOS
domingo, 24 de junio de 2012
martes, 19 de junio de 2012
CASO AUDITORIA ADMINISTRATIVA II
La Señora Rodríguez Realiza una EvaluaciónInterna para Medir el Desempeño del Programa
La señora Rodríguez se estaba preparando para la visita de fin de año de la señora Herná ndez, Coordinadora de Planificación Familiar Estatal del estado de Mendoza. Como supervisora zonal de planificación familiar de la Zona 3, la señora Rodríguez está a cargo de la supervisión de los servicios de planificación familiar en las cuatro clínicas de la zona. La Clínica Costera, ubicada en Puerto Méndez, una ciudad portuaria, cuenta con una enfermera que suministra todos los métodos de planificación familiar ofrecidos por el programa—DIU, píldoras, inyectables y condones. Los clientes que buscan servicios de esterilización son referidos al hospital central de Puerto Méndez. Los clientes que son atendidos en la Clínica Costera tienen familias má s pequeñas y la mayoría de las mujeres ha completado sus estudios secundarios.La Clínica de la Sierra está ubicada en San Felipe, una ciudad con un nú mero de habitantes similar al de
Puerto Méndez. La enfermera del lugar está también capacitada para proveer todos los métodos ofrecidos por el programa y refiere a los clientes que desean servicios de esterilización al hospital de Puerto Méndez. Aproximadamente la mitad de los clientes atendidos por la Clínica de la Sierra han inmigrado recientemente a San Felipe de las á reas rurales. Las dos clínicas rurales — la Occidental y la del Norte—comenzaron a ofrecer servicios en 1995 en un esfuerzo por llegar a la población rural. Ambas clínicas prestan servicios a mujeres que tienden a tener familias numerosas y que son menos educadas que las que acuden a las clínicas urbanas. La enfermera en cada una de estas clínicas suministra píldoras, inyectables y condones y refiere al hospital de Puerto Méndez a aquellos clientes que buscan servicios de esterilización. La Clínica Occidental está ubicada en un pueblo de tamaño mediano en la región geográ fica má s grande de la zona. Los caminos son transitables nueve meses al año, pero es posible que permanezcan cerrados por muchos días durante la época de lluvias. La Clínica del Norte presta servicios a una región má s pequeña que la de la Clínica Occidental, pero tiene una población un poco má s numerosa.
La señora Rodríguez se dio la vuelta cuando escuchó que golpeaban su puerta. "Ah, señora Herná ndez, le ruego que pase y tome asiento" dijo la señora Rodríguez. Las dos mujeres conversaron durante varios minutos mientras tomaban un refresco y luego comenzaron a discutir sobre el desempeño del programa durante el año pasado.
"Cuando nos reunimos para discutir con respecto a diversos temas a principios de este año," comenzó la señora Herná ndez, "nos pusimos de acuerdo en dos objetivos de largo plazo para el programa—aumentar el nú mero de clientes que usan métodos de mayor duración y ampliar la cobertura en las á reas rurales. En base a lo que usted sabe, ¿Piensa que el programa está logrando esos objetivos?"
"Bueno, como usted ya sabe he centrado mis esfuerzos en evaluar nuestro programa este año," respondió la señora Rodríguez. "He revisado todas las estadísticas de servicio recopiladas desde que la Clínica Costera y la Clínica de la Sierra se abrieron a fines de 1993. También he solicitado a cada una de las clínicas que realizara entrevistas a los clientes a la salida de la clínica para determinar el grado de satisfacción de los mismos con los servicios recibidos, y todos hemos participado en la revisión de las cifras de la clínica, de modo que contamos con una buena cantidad de datos. Acabo de completar otra rueda de visitas a las clínicas. En cada una de ellas he sostenido reuniones personales con el fin de discutir sobre el avance logrado y cuá n bien estaban marchando las cosas y si el personal pensaba que la clínica estaba logrando los objetivos de largo plazo del programa."
"Demos un vistazo a las estadísticas de servicio en primer lugar para determinar cuá l ha sido el nivel de desempeño en general para este año," sugirió la señora Herná ndez. Después de revisar las estadísticas, la señora Herná ndez preguntó, "¿Qué supo acerca del desempeño de cada clínica en particular?"
"Me siento tan contenta de que hayamos desarrollado cifras de base para las aceptantes de la píldora y las usuarias de los métodos inyectables. Ahora tenemos un pará metro para medir elprogreso logrado. Habíamos anticipado que durante 1996, podríamos aumentar el nú mero de nuevas usuarias de la píldora a alrededor de 100 y de inyectables a alrededor de 65," continuó la señora Rodríguez. "Como puede ver en base a los datos, no hemos alcanzado esos objetivos. Durante mis reuniones con el personal de la clínica, sostuvimos discusiones con respecto a los hallazgos de los diversos esfuerzos de evaluación, tales como las entrevistas de salida, los aná lisis de las estadísticas de servicio y las observaciones personales. El personal de la Clínica Occidental y la Clínica del Norte acaban de completar una serie de entrevistas de salida que duró todo un mes. Sus hallazgos ayudan a explicar por qué no alcanzaron sus metas. Muchas de las mujeres entrevistadas se quejaban de que les era muy difícil regresar a la clínica con tanta frecuencia para obtener un nuevo suministro de píldoras o hacerse administrar una inyección. Las mujeres que se atendían en la Clínica Occidental dijeron que generalmente les tomaba medio día hacer el viaje y que muchas de sus amigas les habían dicho que estaban interesadas en usar la planificación familiar, pero que no tenían tiempo de efectuar el viaje a la clínica. Usted podrá ver en base a las estadísticas de servicio que el desempeño es bastante consistente entre las dos clínicas rurales, pero no es consistente a nivel de las dos clínicas urbanas. El desempeño en la Clínica de la Sierra ha sido particularmente deficiente. El personal piensa que esto se debe a que prestan servicios a una población numerosa que inmigró de las á reas rurales y que generalmente no está bien informada acerca de la planificación familiar en general y sobre nuestros servicios en particular. La Clínica Costera tienen una buena afluencia de clientes y ha logrado superar sus metas en lo que respecta a la planificación familiar. Sin embargo, la prevalencia de ETS y SIDA constituye una fuente de gran preocupación para el personal, ya que cada vez se diagnostican má s casos por mes."
"Excelente," dijo la señora Herná ndez muy entusiasta, "La felicito por sus esfuerzos de llevar a cabo una evaluación. Al parecer realizó un trabajo exhaustivo de planificación e implementación del proceso de evaluación. Me pregunto si tuvo oportunidad de escuchar las opiniones del personal acerca de lo bien que han respondido a estos problemas y si considera que se necesita realizar má s cambios al programa."
"En cada clínica pasamos un buen tiempo hablando acerca de los cambios que al personal legustaría efectuar en el futuro," dijo la señora Rodríguez. "Durante nuestras discusiones en la Clínica Occidental, el personal sugirió comenzar un programa de distribución comunitaria para responder a las preocupaciones que los clientes habían expresado con respecto a la dificultad de llegar a la clínica. Considero que esto es algo que deberíamos tomar muy en cuenta si deseamos lograr nuestra meta de ampliar nuestra cobertura a las á reas rurales. El personal de las clínicas urbanas sugirió una mejor educación de los clientes y un mayor esfuerzo de extensión, en particular con respecto a las ETS y al SIDA. También algunas mujeres han preguntado si la clínica ofrecía el Norplant®."
La señora Rodríguez sacó una tabla resumida que mostraba las estadísticas de servicio recopiladas durante los ú ltimos tres años y las dos mujeres discutieron en torno al futuro del programa.
|
Estudio de mercado
Buenas tardes, alumnos/as de sexto contabilidad UTC les envió dos enlaces para que ustedes puedan realizar el taller y el estudio de mercado de su proyecto
ESTUDIO DE MERCADO TEORÍA Y TALLER
DIAPOSITIVAS ESTUDIO DE MERCADO
ESTUDIO DE MERCADO TEORÍA Y TALLER
DIAPOSITIVAS ESTUDIO DE MERCADO
jueves, 14 de junio de 2012
ejercicios para todos los terceros de la materia de investigación operativa UTC
UNIVERSIDAD
TÉCNICA DE COTOPAXI
UNIDAD ACADÉMICA
DE CIENCIAS ADMINISTRATIVAS HUMANÍSTICAS
CARRERA DE
INGENIERÍA EN CONTABILIDAD Y AUDITORÍA
EJERCICIOS DE
SOLUCIÓN CON MULTIPLES VARIABLES UTILIZANDO EL WINQSB
1. Una empresa va a lanzar al mercado un nuevo producto. Los planes de
promoción para el próximo mes están en marcha. Los medios alternativos para
realizar la publicidad así como los costos y la audiencia estimada por unidad
de publicidad se muestran a continuación :
TELEVISIÒN
|
RADIO
|
PRENSA
|
|
AUDENCIA POR UNIDAD DE PUBLICIDAD
|
$ 100.000
|
$ 18.000
|
$ 40.000
|
COSTO POR UNIDAD DE PUBLICIDAD
|
$ 2.000
|
$ 300
|
$ 600
|
Para lograr un uso balanceado de los medios, la publicidad en radio
debe ser igual al 50% de unidades de publicidad autorizadas. Además la cantidad
de unidades solicitadas en televisión debe ser al menos 10% del total
autorizado. El presupuesto total para promociones se ha limitado a $ 18.500,00.
Se necesita determinar el plan óptimo para maximizar la audiencia total o
cantidad de personas que vean la publicidad.
2.
Se pretende cultivar en un
terreno dos tipos de olivos: A y B. No se puede cultivar más de 8 has. con
olivos de tipo A, ni más de 10 has. con olivos del tipo B. Cada hectárea de
olivos de tipo A necesita 4 m3 de agua anuales y cada una de tipo B, 3 m3. Se dispone
anualmente de 44 m3 de agua. Cada hectárea de tipo A requiere una inversión de $
500 y cada una de tipo B, $ 225. Se dispone de $ 4500 para realizar dicha
inversión. Si cada hectárea de olivar de tipo A y B producen, respectivamente,
500 y 300 litros anuales de aceite:
a) Obtener
razonadamente las hectáreas de cada tipo de olivo que se deben plantar para
maximizar la producción de aceite.
b) Obtener la producción máxima.
3. La compañía ADEREZO S.A., tiene un stock limitado de dos hierbas que se
utilizan en la producción de aderezos. INDIAN usa los dos ingredientes, HB1 y
HB2, para producir ya sea curry o pimentón. El departamento de mercadotecnia
informa que aunque la empresa puede vender todo el pimentón que pueda producir,
sólo puede vender hasta un máximo de 1500 botellas de curry. Las hierbas no
utilizadas se pueden vender a $375 la onza de HB1 y a $167 la onza de HB2.
Determine él consumo de especias que maximice el ingreso de la Empresa.
4. Una escuela prepara una excursión para 320 alumnos. La empresa de
transporte tiene 10 autobuses de 20 plazas y 8 de 42 plazas, pero sólo dispone
de 9 conductores. El alquiler de un autobús grande cuesta $ 900 y el de uno
pequeño $ 400. Calcular cuántos autobuses de cada tipo hay que utilizar para
que la excursión resulte lo más económica posible para la escuela.
5.
Un establecimiento
de prendas deportivas tiene almacenados 1600 bañadores, 1000 gafas de baño y
800 gorros de baño. Se quiere incentivar la compra de estos productos mediante
la oferta de dos tipos de lotes: el lote A, que produce un beneficio de 8
euros, formado por un bañador, un gorro y unas gafas, y el lote B que produce
un beneficio de $ 10 y está formado por dos bañadores y unas gafas. Sabiendo
que la publicidad de esta oferta tendrá un coste de $ 1.500 a deducir de los
beneficios, se pide calcular el número de lotes A y B que harán máximo el
beneficio y a cuánto asciende éste.
Cuestionario desarrollo de emprendedores
UNIVERSIDAD TÉCNICA
DE COTOPAXI
UNIDAD ACADÉMICA
DE CIENCIAS ADMINISTRATIVAS HUMANÍSTICAS
CARRERA DE
INGENIERÍA EN CONTABILIDAD Y AUDITORÍA
CUESTIONARIO DE DESARROLLO DE EMPRENDEDORES SEGUNDO
PARCIAL
1. Explique 3 características que debe tener el nombre
de la empresa, y un ejemplo de un nombre de un negocio.
2. Explique la
clasificación de una empresa por su giro empresarial.
3. Enuncie 5
ejemplos de empresas de servicios conocidas.
4. Enuncie 5
ejemplos de empresas de comercio conocidas.
5. Enuncie 5
ejemplos de empresas de industrias conocidas.
6. Hable
detalladamente de la misión de la empresa y un ejemplo de una empresa del
sector.
7. Hable
detalladamente de la visión de la empresa y un ejemplo de una empresa del
sector.
8. Explique
detalladamente las tres preguntas básicas, para desarrollar la visión.
9. ¿Cómo se formula los objetivos de la empresa,
explique?
10. ¿Qué
relación o relaciones existe entre los objetivos y la misión empresarial?
11. Explique el
análisis SWOT en forma detallada y concisa.
12. ¿Qué
significa los stakeaholders y 4 ejemplos?
13. La
competencia es una variable del entorno ______________ (complete).
martes, 12 de junio de 2012
ALUMNOS DE SEXTO NIVEL DE DESARROLLO DE EMPRENDEDORES
AQUI ESTA EL ENLACE PARA QUE PUEDAN DESCARGARSE EN PDF
USTEDES DEBEN BASARSE EN ESTOS FORMATOS
EJEMPLO SIMPLIFICADO DE PLAN DE NEGOCIO
EJEMPLO SIMPLIFICADO 2 PLAN DE NEGOCIO
AQUI ESTA EL ENLACE PARA QUE PUEDAN DESCARGARSE EN PDF
USTEDES DEBEN BASARSE EN ESTOS FORMATOS
EJEMPLO SIMPLIFICADO DE PLAN DE NEGOCIO
EJEMPLO SIMPLIFICADO 2 PLAN DE NEGOCIO
sábado, 9 de junio de 2012
Ejercicios UTC programacion lineal solucion multiple
UNIVERSIDAD
TÉCNICA DE COTOPAXI
UNIDAD ACADÉMICA
DE CIENCIAS ADMINISTRATIVAS HUMANÍSTICAS
CARRERA DE
INGENIERÍA EN CONTABILIDAD Y AUDITORÍA
EJERCICIOS DE
PROGRAMACIÓN LINEAL Y SOLUCIÓN MÚLTIPLE
1. Se quiere organizar un puente aéreo
entre dos ciudades, con plazas suficientes de pasaje y carga, para transportar
a 1 600 personas y 96 toneladas de equipaje. Los aviones disponibles son de dos
tipos: 11 del tipo A y 8 del tipo B. La contratación de un avión del tipo A,
que puede transportar a 200 personas y 6 toneladas de equipaje, cuesta $ 40.000;
la contratación de uno del tipo B, que puede transportar a 100 personas y 15
toneladas de equipaje, cuesta $ 10.000. ¿Cuántos aviones de cada tipo deben
utilizarse para que el costo sea mínimo?
2. Un distribuidor de aceite de oliva compra
la materia prima a dos molinos, A y B. Los molinos A y B venden el aceite a $2.000
y $3.000 por tonelada, respectivamente. Cada molino le vende un mínimo de dos
toneladas y un máximo de 7 y para atender a su demanda, el distribuidor debe
comprar en total un mínimo de 6 toneladas. El distribuidor debe comprar como
máximo al molino A, el doble de aceite que al molino B. ¿Qué cantidad de aceite
debe comprar el distribuidor a cada una de los molinos para obtener el mínimo
costo?
2. Una compañía de telefonía móvil quiere
celebrar una jornada de «Consumo razonable» y ofrece a sus clientes la
siguiente oferta: 15 céntimos de dólar por cada mensaje SMS y 25 céntimos de dólar
por cada minuto de conversación incluyendo el costo de establecimiento de
llamada. Impone las condiciones:
a) El número de llamadas de un minuto
no puede ser mayor que el número de mensajes aumentado en 3, ni ser menor que
el número de mensajes disminuido en 3.
b) Sumando el quíntuplo del número de
mensajes con el número de llamadas no puede obtenerse más de 27.
1. Dibuja la región factible.
2. Determina el número de mensajes y
de llamadas para que el beneficio sea máximo.
3.
¿Cuál es ese beneficio máximo?
3. Una fábrica de papel tiene
almacenados 4.000 kg de pasta de papel normal y 3.000 kg de pasta de papel
reciclado. La fábrica produces dos tipos diferentes de cajas de cartón. Para el
primer tipo se utilizan 0,2 kg de pasta de papel normal y
0,1 kg de pasta de papel reciclado, mientras
que para la caja de segundo tipo se utilizan 0,2 kg de pasta de papel normal y
0,3 kg de pasta de papel reciclado.
Los beneficios que la fábrica obtiene
por la venta de cada caja son: respectivamente, $5 para el primer tipo y $6 para el segundo tipo
de cajas.
Utilizando técnicas de programación lineal,
calcula cuántas cajas de cada tipo deben fabricar para obtener el máximo
beneficio. ¿A cuánto asciende el beneficio máximo obtenido?
4. Para dotar de mobiliario urbano a
cierta zona de la ciudad, se quieren colocar al menos 20 piezas entre farolas y
jardineras. Hay 40 farolas y 12 jardineras disponibles. Se pretende que el
número de jardineras colocadas no sea superior a una tercera parte del de
farolas colocadas, pero de forma que por lo menos un 20% de las piezas que se
coloquen sean jardineras.
a) ¿Qué combinaciones de piezas de
cada tipo se pueden colocar? Plantea el problema y representa gráficamente el
conjunto de soluciones.
b) ¿Qué combinación hace que la
diferencia entre el número de farolas y de jardineras colocadas sea mayor? ¿Es
la combinación donde más piezas de mobiliario se colocan?
5. Una fábrica quiere construir
bicicletas de paseo y de montaña. La fábrica dispone de 80 kg de acero y 120 kg
de aluminio. Para construir una bicicleta de paseo se necesitan 1 kg de acero y
3 kg de aluminio y para construir una bicicleta de montaña se necesitan 2 kg de
acero y otros 2 kg de aluminio. Si las bicicletas de paseo las vende a $200 y
las de montaña a $150, ¿cuántas bicicletas de cada tipo debe construir para que
el beneficio sea máximo?
miércoles, 6 de junio de 2012
APUNTES DE FINANZAS EL VALOR DEL DINERO EN EL TIEMPO
1. VALOR DEL DINERO EN EL TIEMPO
El dinero tiene un valor diferente en el tiempo, dado que está afectado por varios factores:
• La inflación que hace que el dinero pierda poder adquisitivo en el tiempo, es decir, que se desvalorice.
• El riesgo en que se incurre al prestar o al invertir, pues no se tiene certeza absoluta de recuperar el dinero prestado o invertido.
• La oportunidad que tendría el dueño del dinero de invertirlo en otra actividad económica, protegiéndolo no sólo de la inflación sino también con la posibilidad de obtener una utilidad.
Por lo expuesto anteriormente, se puede afirmar que no es lo mismo un millón de pesos de hoy a un millón de pesos dentro de un año, pues por los efectos de la inflación, y otras variables económicas, no podemos comprar los mismos bienes de hoy dentro de un año.
De igual manera, podría darse el caso de la persona que invierte un millón de pesos hoy; esta persona al cabo de un año espera recibir un millón de pesos, más un dinero adicional que le permita protegerlo de la inflación y que le genere una utilidad.
Si por ejemplo: un computador, al iniciar el año cuesta $ 2.000.000 y la inflación proyectada para ese año es de 6.5%, quiere decir que para adquirir este mismo computador se debe disponer de $ 2.130.000.
El cálculo puede efectuarse de la siguiente forma:
Nuevo valor = $2000.000 + (2000.000 * 0.065) = $ 2.000.000 (1+ 0.065)
Nuevo valor = $2.000.000 *1.065 = $2.130.000
Dicho de otra forma:
Capital final =V P + (VP*i) = VP *(1+i)
VP: capital inicial
De lo anterior surge el concepto del Valor del Dinero en el Tiempo que sugiere que en nuestras manos y nosotros tomando decisiones con él, el dinero tiene la capacidad de generar más dinero, es decir de generar más valor.
Cuando la riqueza obtenida en un periodo se relaciona con el capital inicialmente comprometido para producirla, obtenemos lo que se denomina tasa de interés. Quiere decir, que lo que un inversionista exige como cantidad diferencial por el hecho de no disponer del dinero ahora a cambio de hacerlo dentro de un periodo determinado, se llama interés, cuya magnitud variará de acuerdo con sus expectativas que él considera está asumiendo al comprometer sus fondos.
2. GENERALIDADES
2.1 CAPITAL
En esta clase el capital es el dinero que se invierte o es prestado.
2.2. INTERES
Para definir el interés nos podemos remitir a algunas definiciones:
• Valor recibido o entregado por el uso del dinero a través del tiempo.
• Utilidad o ganancia que genera un capital.
• Alquiler que se paga por hacer uso del capital ajeno.
• Retribución económica que le devuelve el capital inicial al inversionista.
2.3. TASA DE INTERES
Es la relación que existe entre la utilidad obtenida en un periodo y el capital que inicialmente se comprometió para producir dicha utilidad.
Ejemplo: si una persona invierte hoy la suma de $3.000.000 y al final del año recibe la suma de $3.600.000, ¿cuál fue la tasa de interés que estuvo involucrada en esta inversión?
DATOS:
CAPITAL INICIAL (VP) = $3.000.000
CAPITAL FINAL (VF) = $ 3.6000.000
INTERES EN PSOS ( I ) = VF – VP = $ $3.600.000 - $ 3.000.000
I = $ 600.000
Denotemos la tasa de interés con la letra i
i= I / VP = $ 600.000 / $ 3.000.000
i= 0.20 = 20 %
2.4. TIEMPO
Es el lapso durante el cual se hace uso o se cede el capital y según las partes se pueden dividir en años, meses, semestres, trimestres, días, entre otras.
2.5. POSTULADO DE LAS FINANZAS
Este principio establece que el interés producido por una inversión está en función de tres variables:
• El capital inicial: mientras más grande sea el capital mayor será el interés producido por éste.
• La tasa: ésta depende de las fuerzas del mercado, y esta sujeta al juego de la oferta y la demanda. Cuando hay escasez de dinero las tasas aumenta y cuando hay abundancia de él, las tasas tienden a disminuir.
• El tiempo: mientras mayor sea la duración de la inversión, mayor será el interés producido.
Lo anterior nos permite concluir que para cualquier cálculo de intereses, es absolutamente necesario establecer los valores de las tres variables mencionadas.
3. TIPOS DE INTERES
3.1. INTERES SIMPLE
Se dice que una operación financiera está sujeta al concepto de interés simple, cuando los intereses liquidados periódicamente no se suman al capital, es decir los intereses no generan intereses; por lo cual el capital inicial (VP) permanece constante durante la vigencia de crédito o de la inversión.
NOTA: La tasa de interés simple se aplica sobre el capital inicial, lo que hace que los intereses sean iguales en todos los periodos.
EJEMPLO 1:
Una persona presta $ 4.000.000 al 3% mensual, durante 7 meses. ¿Cuánto se espera recibir de intereses?
DATOS:
VP = $ 4.000.000
i= 3% mensual = 0.03
TIEMPO (n) = 7 meses
I =?
Solución:
Tenemos que
I = $ 4.000.000 * 0.03 * 7
I = $ 840.000
Respuesta, el interés producido por $ 4.000.000 al 3% mensual durante 7 meses es $ 840.000.
Nota: la tasa de interés y el tiempo tienen que estar en la misma base, es decir, si los intereses son mensuales el tiempo tiene que ser mensual; si es bimestral el tiempo es bimestral.
EJEMPLO 2:
Un CDT de $5.000.000 paga un interés del 2.8% trimestral simple; cuánto genera en concepto de intereses en un año.
DATOS
VP = $ 5.000.000
i= 2.8 % trimestral
n = 1 año = 4 trimestres.
Solución
I = $ 5.000.000 * 0.028 *4
I = $ 560.000
Respuesta, un CDT de $ 5.000.000 colocados al 2.8% trimestral durante un año genera un interés de $ 560.000
EJEMPLO 3:
Una inversión generó un interés de $ 1.250.000 durante 3 años, si la tasa de interés que se reconoció por esta inversión fue el 2.3% mensual, ¿cuál fue el capital que inicialmente se invirtió?
DATOS:
I = $ 1.250.000
i= 2.3% mensual 0.023
n = 3 años = 36 meses
Solución
Por formula general tenemos que
Se despeja de la formula VP,
VP = I / (i * n) entonces,
VP = $1.250.000 / (0.023 * 36)
VP = $ 1.250.000/ 0.828
VP = $ 1.509.661, 84
Respuesta, para que una inversión produzca un $ 1.250.000 de interés, durante tres años a una tasa del 2,3% su capital inicial debe ser $1.509.661.84
EJEMPLO 4:
Durante cuanto tiempo estuvo invertido un capital de $10.000.000 para que al 4% bimestral produjera $ 6.700.000 de intereses.
DATOS
VP = $ 10.000.000
I= $ 6.700.000
i= 4% bimestral = 0.04
n = ?
Por fórmula general tenemos que
Despejamos de la formula,
n= I / (VP * i) entonces
n = $ 6.700.000 / ($ 10.000.000 *0.04)
n = $ 6.700.000 / $400.000
n= 16.75 bimestres
Respuesta, el tiempo que se necesita para un capital de $10.000.000 produzca $ 6.700.000 de interese a una tasa de 4 % bimestral es de 16,75 bimestres.
EJEMPLO 5:
Una persona realizo una inversión de $ 12.000.000 y al año y medio recibió de intereses la suma de $ 1.370.000, cual fue la rentabilidad mensual de esta inversión.
DATOS:
VP = $ 12.000.000
I = $ 1.370.000
n = 1, 5 años = 18 meses
i= ?
Por formula general tenemos que
Despejamos i
i= I /( VP*n)
Entonces,
i= $ 1.370.000 / ($12.000.000 * 18)
i = $ 1.370.000 / $216.000.000
i = 0.00634 equivalente a 0.634% mensual.
NOTA: Cuando la respuesta sea en tasa de interés, esta se debe dar en términos porcentuales.
EJEMPLO 6:
¿Qué suma tendrá que pagar una persona al término de 3 años, si en este momento le prestan $7.500.000 al 5% semestralmente y se debe pagar al final los intereses y el capital?
Antes de solucionar el ejercicio, cabe aclarar que en ocasiones no se pagan periódicamente los intereses sino que se pacta desde el inicio, entre las partes, el pago de los intereses y el capital al finalizar el vencimiento del plazo, esto es conocido como monto o valor final o valor futuro y lo denominamos VF.
Se denomina monto o valor futuro al capital inicial (VP) más los intereses (I), entonces:
VF = VP + I
Recordar que I = VP * i * n
Reemplazamos en la fórmula,
VF = VP + (VP * i * n)
VF = VP * (1+ (i*n))
Solución del ejercicio
DATOS:
n = 3 años = 6 semestres.
VP = $ 7.500.000
i= 5% semestral 0,05
VF = ?
Tenemos que
VF = $7.500.000 * ( 1 + ( 0,05 * 6)
VF = $ 7.500.000 * ( 1 + ( 0,3))
VF = $7.500.000 * 1,3
VF = $ 9.750.000
Respuesta, al termino de tres años, una persona que presta $7.500.000 al 5% semestral debe pagar al vencimiento $ 9,750.000.
EJEMPLO 7:
Calcule el monto a recibir en nueve meses por ahorrar $ 1.000.000 hoy, con una tasa de interés del 8,5% anual.
DATOS.
VP = $ 1.000.000
i= 8,5% anual 0,085
n = 9 meses = 9/360 = 0,025
VF= ?
Utilizamos la fórmula
VF = $ 1.000.000 * ( 1+ (0,085 * 0,025))
VF = $ 1.000.000 * 1.002125
VF = $ 1.002.125
Respuesta, por ahorrar $1.000.000 hoy, a una tasa de interés del 8,5% anual por nueve meses recibe $ 1.002.125.
EJEMPLO 8:
Un crédito tiene un valor al vencimiento de $90.000 ¿Cuál será el valor presente en 60 días antes del vencimiento? Suponga una tasa de interés del 28% anual.
DATOS
VF = $ 90.000
n= 60 días = 60 / 360 = 0,166666666
i= 28% 0,28
VP = ?
Solución
Sabemos que
Despejamos de la fórmula
VP = VF / (1+ (i*n)) entonces,
VP = $ 90.000 / (1+ (0,28 * 0,166666666))
VP = $ 90.000 / (1,046666667)
VP = $ 85.987, 26
Respuesta, el valor presente de un crédito que estaba al 28% en 60 días es de $85.987, 26.
FORMULAS DE INTERES SIMPLE
Fórmula 1 Interés simple I = VP * i * n
Fórmula 2 Valor Presente o Valor Actual VP = I /( i * n)
Fórmula 3 Tasa de Interés i = I / ( VP *n)
Fórmula 4 Número de Periodos n = I / (VP * i)
Fórmula 5 Monto o Valor Futuro VF = VP * (1 + i* n )
3.2. INTERES COMPUESTO
La gran mayoría de las operaciones financieras se realizan a interés compuesto con el objeto de tener en cuenta que los intereses liquidados no entregados, entran a formar parte del capital y para próximos periodos generarán a su vez intereses. Este fenómeno se conoce con el nombre de Capitalización de Intereses.
La diferencia fundamental que existe entre el interés simple y el interés compuesto consiste en que el interés simple liquida los intereses cada período y se pagan inmediatamente; en el interés compuesto los intereses liquidados se acumulan al capital para formar un nuevo capital denominado Monto y sobre este monto se calculan los nuevos intereses del siguiente periodo.
Supongamos que una persona invierte $1.000.000 en un CDT a 4 meses, a una tasa del 0.9% mensual, con liquidación mensual de intereses. ¿Cuánto dinero recibirá la persona al cabo de los 4 meses cuando se haya madurado el CDT?
El cálculo puede ilustrarse en la siguiente tabla:
Observemos el procedimiento paso por paso para que tratemos de deducir una fórmula que nos permita calcular directamente el monto final.
0 1 2 3 n
/__________/__________________/________________ / ______________/
VP VF1 = VP + I VF2 = VF1 + VF1 *i*n VF3 = VF2 + VF2 *i*n
I VF1 = VP + VP * i *n VF2 = VF1* (1+ i) VF3 = VF2* (1+ i)
VF1 = VP * (1 + i) VF2 = VP (1+i) * (1+i) VF3 = VP (1+i)2 * (1+i)
VF2 = VP (1+ i)2 VF3 = VP (1+ i)3
Como se acumula período a período, la n va tomando el valor de uno, y los intereses de cada período se liquidan sobre el monto anterior.
De acuerdo al anterior desarrollo, si continuamos y llegamos al periodo 15 el valor futuro es:
VF 15 = VP (1+ i) 15
Podemos concluir que a los n periodos el monto o valor futuro será:
VF = VP (1 + i) n
EJEMPLO 9:
Un capital de $36.000.000 estuvo invertido 3 años, al 28% anual compuesto. ¿Cuál fue su monto o valor futuro?
DATOS:
VP = $ 36.000.000
n= 3 años
i= 28% 0,28
VF = ?
Solución
Sabemos que
Reemplazamos en la fórmula.
VF = $ 36.000.000 (1 + 0,28) 3
VF = $ 36.000.000 * 2,097152
VF = $ 75.497.472
Respuesta, un capital de $36.000.000 invertido hoy al 28% anual durante 3 años equivale a $75.497.472.
EJEMPLO 10:
Una persona desea disponer de $3.000.000 dentro de dos años. ¿Cuánto debe invertir hoy para cumplir su objetivo, si la tasa de interés que le reconoce la entidad financiera es del 18% anual con capitalización mensual?
DATOS.
VF = $ 3.000.0000
n = 2 años 24 meses
i = 18% anual con capitalización mensual 18%/12 = 1.5% mensual
Nota: recordemos que la tasa de interés y el tiempo siempre deben de estar en la misma base. Cuando se habla de capitalización se esta indicando que los intereses se suman al capital de acuerdo al periodo de referencia.
Ejemplo. Si decimos que se tiene una tasa de interés del 30% anual con capitalización bimestral, entonces los periodos de referencia son 6 bimestres puesto que seis corresponde a los bimestres que tiene un año.
Solución al ejercicio
Sabemos que
Despejamos la fórmula,
VP = VF / (1+ i) n
Entonces,
VP = $ 3.000.000 / (1 + 0.015) 24
VP = $ 3.000.000 / 1,429502812
VP = $ 2.098.631, 75
Respuesta, si una persona quiere disponer de $3.000.000 dentro de dos años a una tasa del 18% anual con capitalización mensual debe invertir hoy $2.098.631,75
EJEMPLO 11:
Una persona invierte $5.000.000 durante año y medio con intereses liquidados y capitalizados mensualmente y le entregan al final $6.250.000. ¿Cual fue la tasa de interés que le reconocieron en esta inversión?
DATOS
VP = $ 5.000.000
VF = $ 6.250.000
n= 1, 5 años = 18 meses
i= ?
Sabemos que:
Despejamos de la fórmula,
VF / VP = (1 + i)n
Para poder despejar el interés se saca raíz cuadrada de n a ambos lados.
n√VF/ VP = (1+i)
i= (n√VF/ VP ) – 1
i = ( 18√$6.250.000/ $ 5.000.000) – 1
i = 1.012474024 -1
i = 0,012474 = 1, 2474% mensuales.
Respuesta, la tasa de interés que se reconoce en una inversión de $5.000.000 a un año y medio con periodos de capitalización mensuales, es de 1,2474% mensual.
EJEMPLO 12:
Una persona tomo prestado $10.000.000 a una tasa de interés del 2% mensual compuesto, y al final del crédito pagó $41.611.403, 75 ¿qué plazo le concedieron?
DATOS:
VP = $ 10.000.000
VF = $ 41.611.403,75
i= 2% mensual
n = ?
Sabemos que
Despejamos la variable n,
VF / VP = (1 + i) n
Por las propiedades de la potenciación, para despejar la n debemos utilizar los logaritmos, así.
Log (VF/VP) = n log (1+i)
n = log (VF/ VP) / log (1+ i)
n = log ($41.611.403,75/ $10.000.000) /log ( 1+ 0,02)
n = 72 meses = 6 años
Respuesta, el tiempo que le concedieron en este crédito es de 72 meses equivalente a 6 años.
FORMULAS DE INTERES COMPUESTO
Fórmula 1 Monto o Valor Futuro VF = VP x (1 + i ) n
Fórmula 2 Valor Presente o Valor Actual VP = VF /( 1 + i ) n
Fórmula 3 Tasa de Interés i = ( VF / VP) 1/n – 1
Fórmula 4 Número de Periodos n = log (VF/VP)/log (1+i)
Formula 5 Interés compuesto I = VP ((1+i)n – 1)
Todas los ejemplos anteriores se pueden realizar utilizando Calculadora Financiera o las funciones financieras del Excel. Estas herramientas deben considerarse con un instrumento para facilitar los cálculos pues su manejo, más que un proceso mecánico, es un proceso racional en el sentido de que la clave está en plantear adecuadamente el problema que se requiere resolver, para luego plasmarla en forma de instrucciones a la maquina o computador.
El dinero tiene un valor diferente en el tiempo, dado que está afectado por varios factores:
• La inflación que hace que el dinero pierda poder adquisitivo en el tiempo, es decir, que se desvalorice.
• El riesgo en que se incurre al prestar o al invertir, pues no se tiene certeza absoluta de recuperar el dinero prestado o invertido.
• La oportunidad que tendría el dueño del dinero de invertirlo en otra actividad económica, protegiéndolo no sólo de la inflación sino también con la posibilidad de obtener una utilidad.
Por lo expuesto anteriormente, se puede afirmar que no es lo mismo un millón de pesos de hoy a un millón de pesos dentro de un año, pues por los efectos de la inflación, y otras variables económicas, no podemos comprar los mismos bienes de hoy dentro de un año.
De igual manera, podría darse el caso de la persona que invierte un millón de pesos hoy; esta persona al cabo de un año espera recibir un millón de pesos, más un dinero adicional que le permita protegerlo de la inflación y que le genere una utilidad.
Si por ejemplo: un computador, al iniciar el año cuesta $ 2.000.000 y la inflación proyectada para ese año es de 6.5%, quiere decir que para adquirir este mismo computador se debe disponer de $ 2.130.000.
El cálculo puede efectuarse de la siguiente forma:
Nuevo valor = $2000.000 + (2000.000 * 0.065) = $ 2.000.000 (1+ 0.065)
Nuevo valor = $2.000.000 *1.065 = $2.130.000
Dicho de otra forma:
Capital final =V P + (VP*i) = VP *(1+i)
VP: capital inicial
De lo anterior surge el concepto del Valor del Dinero en el Tiempo que sugiere que en nuestras manos y nosotros tomando decisiones con él, el dinero tiene la capacidad de generar más dinero, es decir de generar más valor.
Cuando la riqueza obtenida en un periodo se relaciona con el capital inicialmente comprometido para producirla, obtenemos lo que se denomina tasa de interés. Quiere decir, que lo que un inversionista exige como cantidad diferencial por el hecho de no disponer del dinero ahora a cambio de hacerlo dentro de un periodo determinado, se llama interés, cuya magnitud variará de acuerdo con sus expectativas que él considera está asumiendo al comprometer sus fondos.
2. GENERALIDADES
2.1 CAPITAL
En esta clase el capital es el dinero que se invierte o es prestado.
2.2. INTERES
Para definir el interés nos podemos remitir a algunas definiciones:
• Valor recibido o entregado por el uso del dinero a través del tiempo.
• Utilidad o ganancia que genera un capital.
• Alquiler que se paga por hacer uso del capital ajeno.
• Retribución económica que le devuelve el capital inicial al inversionista.
2.3. TASA DE INTERES
Es la relación que existe entre la utilidad obtenida en un periodo y el capital que inicialmente se comprometió para producir dicha utilidad.
Ejemplo: si una persona invierte hoy la suma de $3.000.000 y al final del año recibe la suma de $3.600.000, ¿cuál fue la tasa de interés que estuvo involucrada en esta inversión?
DATOS:
CAPITAL INICIAL (VP) = $3.000.000
CAPITAL FINAL (VF) = $ 3.6000.000
INTERES EN PSOS ( I ) = VF – VP = $ $3.600.000 - $ 3.000.000
I = $ 600.000
Denotemos la tasa de interés con la letra i
i= I / VP = $ 600.000 / $ 3.000.000
i= 0.20 = 20 %
2.4. TIEMPO
Es el lapso durante el cual se hace uso o se cede el capital y según las partes se pueden dividir en años, meses, semestres, trimestres, días, entre otras.
2.5. POSTULADO DE LAS FINANZAS
Este principio establece que el interés producido por una inversión está en función de tres variables:
• El capital inicial: mientras más grande sea el capital mayor será el interés producido por éste.
• La tasa: ésta depende de las fuerzas del mercado, y esta sujeta al juego de la oferta y la demanda. Cuando hay escasez de dinero las tasas aumenta y cuando hay abundancia de él, las tasas tienden a disminuir.
• El tiempo: mientras mayor sea la duración de la inversión, mayor será el interés producido.
Lo anterior nos permite concluir que para cualquier cálculo de intereses, es absolutamente necesario establecer los valores de las tres variables mencionadas.
3. TIPOS DE INTERES
3.1. INTERES SIMPLE
Se dice que una operación financiera está sujeta al concepto de interés simple, cuando los intereses liquidados periódicamente no se suman al capital, es decir los intereses no generan intereses; por lo cual el capital inicial (VP) permanece constante durante la vigencia de crédito o de la inversión.
NOTA: La tasa de interés simple se aplica sobre el capital inicial, lo que hace que los intereses sean iguales en todos los periodos.
EJEMPLO 1:
Una persona presta $ 4.000.000 al 3% mensual, durante 7 meses. ¿Cuánto se espera recibir de intereses?
DATOS:
VP = $ 4.000.000
i= 3% mensual = 0.03
TIEMPO (n) = 7 meses
I =?
Solución:
Tenemos que
I = $ 4.000.000 * 0.03 * 7
I = $ 840.000
Respuesta, el interés producido por $ 4.000.000 al 3% mensual durante 7 meses es $ 840.000.
Nota: la tasa de interés y el tiempo tienen que estar en la misma base, es decir, si los intereses son mensuales el tiempo tiene que ser mensual; si es bimestral el tiempo es bimestral.
EJEMPLO 2:
Un CDT de $5.000.000 paga un interés del 2.8% trimestral simple; cuánto genera en concepto de intereses en un año.
DATOS
VP = $ 5.000.000
i= 2.8 % trimestral
n = 1 año = 4 trimestres.
Solución
I = $ 5.000.000 * 0.028 *4
I = $ 560.000
Respuesta, un CDT de $ 5.000.000 colocados al 2.8% trimestral durante un año genera un interés de $ 560.000
EJEMPLO 3:
Una inversión generó un interés de $ 1.250.000 durante 3 años, si la tasa de interés que se reconoció por esta inversión fue el 2.3% mensual, ¿cuál fue el capital que inicialmente se invirtió?
DATOS:
I = $ 1.250.000
i= 2.3% mensual 0.023
n = 3 años = 36 meses
Solución
Por formula general tenemos que
Se despeja de la formula VP,
VP = I / (i * n) entonces,
VP = $1.250.000 / (0.023 * 36)
VP = $ 1.250.000/ 0.828
VP = $ 1.509.661, 84
Respuesta, para que una inversión produzca un $ 1.250.000 de interés, durante tres años a una tasa del 2,3% su capital inicial debe ser $1.509.661.84
EJEMPLO 4:
Durante cuanto tiempo estuvo invertido un capital de $10.000.000 para que al 4% bimestral produjera $ 6.700.000 de intereses.
DATOS
VP = $ 10.000.000
I= $ 6.700.000
i= 4% bimestral = 0.04
n = ?
Por fórmula general tenemos que
Despejamos de la formula,
n= I / (VP * i) entonces
n = $ 6.700.000 / ($ 10.000.000 *0.04)
n = $ 6.700.000 / $400.000
n= 16.75 bimestres
Respuesta, el tiempo que se necesita para un capital de $10.000.000 produzca $ 6.700.000 de interese a una tasa de 4 % bimestral es de 16,75 bimestres.
EJEMPLO 5:
Una persona realizo una inversión de $ 12.000.000 y al año y medio recibió de intereses la suma de $ 1.370.000, cual fue la rentabilidad mensual de esta inversión.
DATOS:
VP = $ 12.000.000
I = $ 1.370.000
n = 1, 5 años = 18 meses
i= ?
Por formula general tenemos que
Despejamos i
i= I /( VP*n)
Entonces,
i= $ 1.370.000 / ($12.000.000 * 18)
i = $ 1.370.000 / $216.000.000
i = 0.00634 equivalente a 0.634% mensual.
NOTA: Cuando la respuesta sea en tasa de interés, esta se debe dar en términos porcentuales.
EJEMPLO 6:
¿Qué suma tendrá que pagar una persona al término de 3 años, si en este momento le prestan $7.500.000 al 5% semestralmente y se debe pagar al final los intereses y el capital?
Antes de solucionar el ejercicio, cabe aclarar que en ocasiones no se pagan periódicamente los intereses sino que se pacta desde el inicio, entre las partes, el pago de los intereses y el capital al finalizar el vencimiento del plazo, esto es conocido como monto o valor final o valor futuro y lo denominamos VF.
Se denomina monto o valor futuro al capital inicial (VP) más los intereses (I), entonces:
VF = VP + I
Recordar que I = VP * i * n
Reemplazamos en la fórmula,
VF = VP + (VP * i * n)
VF = VP * (1+ (i*n))
Solución del ejercicio
DATOS:
n = 3 años = 6 semestres.
VP = $ 7.500.000
i= 5% semestral 0,05
VF = ?
Tenemos que
VF = $7.500.000 * ( 1 + ( 0,05 * 6)
VF = $ 7.500.000 * ( 1 + ( 0,3))
VF = $7.500.000 * 1,3
VF = $ 9.750.000
Respuesta, al termino de tres años, una persona que presta $7.500.000 al 5% semestral debe pagar al vencimiento $ 9,750.000.
EJEMPLO 7:
Calcule el monto a recibir en nueve meses por ahorrar $ 1.000.000 hoy, con una tasa de interés del 8,5% anual.
DATOS.
VP = $ 1.000.000
i= 8,5% anual 0,085
n = 9 meses = 9/360 = 0,025
VF= ?
Utilizamos la fórmula
VF = $ 1.000.000 * ( 1+ (0,085 * 0,025))
VF = $ 1.000.000 * 1.002125
VF = $ 1.002.125
Respuesta, por ahorrar $1.000.000 hoy, a una tasa de interés del 8,5% anual por nueve meses recibe $ 1.002.125.
EJEMPLO 8:
Un crédito tiene un valor al vencimiento de $90.000 ¿Cuál será el valor presente en 60 días antes del vencimiento? Suponga una tasa de interés del 28% anual.
DATOS
VF = $ 90.000
n= 60 días = 60 / 360 = 0,166666666
i= 28% 0,28
VP = ?
Solución
Sabemos que
Despejamos de la fórmula
VP = VF / (1+ (i*n)) entonces,
VP = $ 90.000 / (1+ (0,28 * 0,166666666))
VP = $ 90.000 / (1,046666667)
VP = $ 85.987, 26
Respuesta, el valor presente de un crédito que estaba al 28% en 60 días es de $85.987, 26.
FORMULAS DE INTERES SIMPLE
Fórmula 1 Interés simple I = VP * i * n
Fórmula 2 Valor Presente o Valor Actual VP = I /( i * n)
Fórmula 3 Tasa de Interés i = I / ( VP *n)
Fórmula 4 Número de Periodos n = I / (VP * i)
Fórmula 5 Monto o Valor Futuro VF = VP * (1 + i* n )
3.2. INTERES COMPUESTO
La gran mayoría de las operaciones financieras se realizan a interés compuesto con el objeto de tener en cuenta que los intereses liquidados no entregados, entran a formar parte del capital y para próximos periodos generarán a su vez intereses. Este fenómeno se conoce con el nombre de Capitalización de Intereses.
La diferencia fundamental que existe entre el interés simple y el interés compuesto consiste en que el interés simple liquida los intereses cada período y se pagan inmediatamente; en el interés compuesto los intereses liquidados se acumulan al capital para formar un nuevo capital denominado Monto y sobre este monto se calculan los nuevos intereses del siguiente periodo.
Supongamos que una persona invierte $1.000.000 en un CDT a 4 meses, a una tasa del 0.9% mensual, con liquidación mensual de intereses. ¿Cuánto dinero recibirá la persona al cabo de los 4 meses cuando se haya madurado el CDT?
El cálculo puede ilustrarse en la siguiente tabla:
Observemos el procedimiento paso por paso para que tratemos de deducir una fórmula que nos permita calcular directamente el monto final.
0 1 2 3 n
/__________/__________________/________________ / ______________/
VP VF1 = VP + I VF2 = VF1 + VF1 *i*n VF3 = VF2 + VF2 *i*n
I VF1 = VP + VP * i *n VF2 = VF1* (1+ i) VF3 = VF2* (1+ i)
VF1 = VP * (1 + i) VF2 = VP (1+i) * (1+i) VF3 = VP (1+i)2 * (1+i)
VF2 = VP (1+ i)2 VF3 = VP (1+ i)3
Como se acumula período a período, la n va tomando el valor de uno, y los intereses de cada período se liquidan sobre el monto anterior.
De acuerdo al anterior desarrollo, si continuamos y llegamos al periodo 15 el valor futuro es:
VF 15 = VP (1+ i) 15
Podemos concluir que a los n periodos el monto o valor futuro será:
VF = VP (1 + i) n
EJEMPLO 9:
Un capital de $36.000.000 estuvo invertido 3 años, al 28% anual compuesto. ¿Cuál fue su monto o valor futuro?
DATOS:
VP = $ 36.000.000
n= 3 años
i= 28% 0,28
VF = ?
Solución
Sabemos que
Reemplazamos en la fórmula.
VF = $ 36.000.000 (1 + 0,28) 3
VF = $ 36.000.000 * 2,097152
VF = $ 75.497.472
Respuesta, un capital de $36.000.000 invertido hoy al 28% anual durante 3 años equivale a $75.497.472.
EJEMPLO 10:
Una persona desea disponer de $3.000.000 dentro de dos años. ¿Cuánto debe invertir hoy para cumplir su objetivo, si la tasa de interés que le reconoce la entidad financiera es del 18% anual con capitalización mensual?
DATOS.
VF = $ 3.000.0000
n = 2 años 24 meses
i = 18% anual con capitalización mensual 18%/12 = 1.5% mensual
Nota: recordemos que la tasa de interés y el tiempo siempre deben de estar en la misma base. Cuando se habla de capitalización se esta indicando que los intereses se suman al capital de acuerdo al periodo de referencia.
Ejemplo. Si decimos que se tiene una tasa de interés del 30% anual con capitalización bimestral, entonces los periodos de referencia son 6 bimestres puesto que seis corresponde a los bimestres que tiene un año.
Solución al ejercicio
Sabemos que
Despejamos la fórmula,
VP = VF / (1+ i) n
Entonces,
VP = $ 3.000.000 / (1 + 0.015) 24
VP = $ 3.000.000 / 1,429502812
VP = $ 2.098.631, 75
Respuesta, si una persona quiere disponer de $3.000.000 dentro de dos años a una tasa del 18% anual con capitalización mensual debe invertir hoy $2.098.631,75
EJEMPLO 11:
Una persona invierte $5.000.000 durante año y medio con intereses liquidados y capitalizados mensualmente y le entregan al final $6.250.000. ¿Cual fue la tasa de interés que le reconocieron en esta inversión?
DATOS
VP = $ 5.000.000
VF = $ 6.250.000
n= 1, 5 años = 18 meses
i= ?
Sabemos que:
Despejamos de la fórmula,
VF / VP = (1 + i)n
Para poder despejar el interés se saca raíz cuadrada de n a ambos lados.
n√VF/ VP = (1+i)
i= (n√VF/ VP ) – 1
i = ( 18√$6.250.000/ $ 5.000.000) – 1
i = 1.012474024 -1
i = 0,012474 = 1, 2474% mensuales.
Respuesta, la tasa de interés que se reconoce en una inversión de $5.000.000 a un año y medio con periodos de capitalización mensuales, es de 1,2474% mensual.
EJEMPLO 12:
Una persona tomo prestado $10.000.000 a una tasa de interés del 2% mensual compuesto, y al final del crédito pagó $41.611.403, 75 ¿qué plazo le concedieron?
DATOS:
VP = $ 10.000.000
VF = $ 41.611.403,75
i= 2% mensual
n = ?
Sabemos que
Despejamos la variable n,
VF / VP = (1 + i) n
Por las propiedades de la potenciación, para despejar la n debemos utilizar los logaritmos, así.
Log (VF/VP) = n log (1+i)
n = log (VF/ VP) / log (1+ i)
n = log ($41.611.403,75/ $10.000.000) /log ( 1+ 0,02)
n = 72 meses = 6 años
Respuesta, el tiempo que le concedieron en este crédito es de 72 meses equivalente a 6 años.
FORMULAS DE INTERES COMPUESTO
Fórmula 1 Monto o Valor Futuro VF = VP x (1 + i ) n
Fórmula 2 Valor Presente o Valor Actual VP = VF /( 1 + i ) n
Fórmula 3 Tasa de Interés i = ( VF / VP) 1/n – 1
Fórmula 4 Número de Periodos n = log (VF/VP)/log (1+i)
Formula 5 Interés compuesto I = VP ((1+i)n – 1)
Todas los ejemplos anteriores se pueden realizar utilizando Calculadora Financiera o las funciones financieras del Excel. Estas herramientas deben considerarse con un instrumento para facilitar los cálculos pues su manejo, más que un proceso mecánico, es un proceso racional en el sentido de que la clave está en plantear adecuadamente el problema que se requiere resolver, para luego plasmarla en forma de instrucciones a la maquina o computador.
martes, 13 de marzo de 2012
DIFERENCIAS ENTRE FINANZAS INTERNACIONALES Y FINANZAS CORPORTATIVAS
Las
finanzas
constituyen una rama de la economía
que se encarga de la administración
del dinero. Las finanzas
internacionales, por lo tanto, estudian el flujo de
efectivo entre distintos países.
Esta
disciplina
puede dividirse en dos ramas de estudio: la economía internacional (que tiene
en cuenta el tipo de
cambio, las tasas de interés y otros aspectos financieros) y
las finanzas
corporativas (el estudio de los mercados y los productos
financieros).
Ante
el fenómeno de la globalización,
que implica el libre movimiento de capitales y el levantamiento de distintos
tipos de restricciones (físicas, aduaneras, impositivas), las finanzas
internacionales han adquirido particular importancia.
Un
concepto importante dentro de este ámbito es el de divisa, que es la
moneda de un país
que es convertible en moneda de otro extranjero en el mercado cambiario. Para
esto, existe la convertibilidad
interna (la posibilidad de comprar y vender monedas extranjeras
en un país) y la convertibilidad
externa (la cotización de una moneda nacional en los mercados
cambiarios de otros países).
Este
tipo de cambio
puede ser fijo
(cuando el banco central estable el valor de la moneda e interviene en el
mercado cambiario) o flexible
(el banco central no interviene en el mercado, por lo que el valor de la moneda
queda sujeto al libre juego de la oferta y la demanda).
Por
otra parte, cabe destacar que se conoce como balanza de pagos al saldo de
todas las transacciones económicas de un país con el resto del mundo. En ella
se registran los ingresos y los egresos de divisas.
AUTOR: http://definicion.de/finanzas-internacionales/
lunes, 12 de marzo de 2012
DIFERENCIAS ENTRE CARRERAS DE COMPUTACIÓN, INFORMÁTICA, INGENIERÍA DE SOFTWARE
En esta sección, caracterizamos cada uno de las cinco grandes disciplinas en computación. Disculpen si la lectura es un poco tediosa.
Computer Engineering (Ingeniería de Computadoras)
La
Ingeniería de Computadoras está interesada en el diseño y construcción
de computadoras y sistemas basados en computadoras. Esto involucra el
estudio del hardware, software, comunicaciones, y la interacción entre
ellos. Su currículo se enfoca en las teorías, principios, y prácticas de
la Ingeniería Eléctrica tradicional y las matemáticas, y aplica estas a
los problemas de diseñar computadoras y dispositivos basados en computadoras.
Los
estudiantes de Ingeniería de Computadoras estudian el diseño de
sistemas hardware digitales, incluyendo computadoras, sistemas de
comunicación, y dispositivos que contienen computadoras. Ellos también
estudian el desarrollo del software enfocado en el software usado dentro
y entre dispositivos digitales (no programas de software directamente
usados por usuarios). El currículo enfatiza más hardware que software, y tiene un fuerte sabor a Ingeniería.
Actualmente,
un área dominante dentro de la Ingeniería de Computadoras es la de
sistemas embebidos, el desarrollo de dispositivos que tienen componentes
software embebidos en hardware. Por ejemplo, dispositivos tales como
teléfonos celulares, equipos de audio digital, equipos de video digital,
sistemas de alarma, máquinas de rayos X, y herramientas láser de
cirugía requieren la integración de hardware y software embebido, y
todas ellas son el resultado de la Ingeniería de Computadoras.
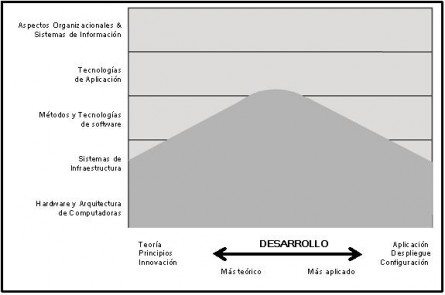
Computer Science (Ciencias de la Computación)
Las
Ciencias de la Computación abarca un amplio rango, desde sus
fundamentos teóricos y algorítmicos hasta avanzados desarrollos en
robótica, visión por computadora, sistemas inteligentes, bioinformática,
y otras excitantes áreas. Podemos pensar que el trabajo de los
científicos de la computación cae en tres categorías:
Ellos diseñan e implementan software.
Los científicos de la computación afrontan desafiantes tareas de
programación desafiantes. Ellos también supervisan a otros
programadores, manteniéndolos informados de nuevas avances.
Ellos
crean nuevas maneras de usar las computadoras. Progreso de las Ciencias
de la Computación en las áreas de Networking, Bases de Datos, e
interface humano-computadora permitieron el desarrollo del World Wide
Web. Ahora, los investigadores están trabajando para hacer que los
robots sean ayudantes prácticos que demuestren inteligencia, están
usando bases de datos para crear nuevo conocimiento, y están usando computadoras para ayudar a descifrar los secretos de nuestro ADN.
Ellos
desarrollan maneras efectivas de resolver problemas de computación. Por
ejemplo, los científicos en computación desarrollan las mejores
posibles maneras de almacenar información en bases de datos, enviar
datos a través de las redes, y mostrar imágenes complejas. Su base
teórica les permite determinar la mejor performance posible, y sus
estudios de algoritmos les ayudan a desarrollar nuevas métodos que
proporcionen mejores performances.
Las
Ciencias de la Computación abarca el rango de la teoría a la
programación. Mientras otras disciplinas pueden producir graduados mejor
preparados para trabajos específicos, las Ciencias de la Computación
ofrecen una fundamentación amplia y completa que permite a los graduados
adaptarse a nuevas tecnologías y nuevas ideas.
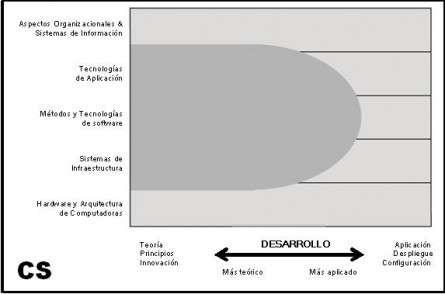
Information Systems (Sistemas de Información)
Los
especialistas en Sistemas de Información se enfocan en integrar las
soluciones en tecnologías de información y los procesos de los negocios
para cumplir con las necesidades de información de los negocios y otras
organizaciones, permitiéndoles alcanzar sus objetivos de una manera
efectiva y eficiente. La perspectiva de esta disciplina en la
“tecnología de información” enfatiza en la información, y ve a la
tecnología como un instrumento que permite la generación, procesamiento y
distribución de la información necesitada. Los profesionales en esta
disciplina están principalmente involucrados con la información que los
sistemas de computadoras pueden proporcionar para ayudar a una empresa
en definir y alcanzar sus metas, y los procesos que una empresa puede
implementar y mejorar usando tecnologías de información. Ellos deben
comprender tanto factores técnicos como organizacionales, y deben ser
capaces de ayudar a una organización en determinar como la información y
los procesos de negocios facilitados por la tecnología pueden
proporcionar una ventaja competitiva.
Los
especialistas en sistemas de información juegan un rol clave en
determinar los requerimientos de los sistemas de información de una
organización y está inmerso en su especificación, diseño, e
implementación. Como resultado, tales profesionales requieren de un
sólido entendimiento de los principios y prácticas organizacionales de
manera que puedan servir como un puente efectivo entre las comunidades
técnicas y administrativas de una organización, permitiendo a ellos
trabajar en armonía para asegurar que la organización tiene la
información y los sistemas que necesita para soportar sus operaciones.
Los profesionales en sistemas de información también están involucrados
en diseñar sistemas de comunicación y colaboración organizacional
basados en tecnologías.
Una
mayoría de programas de Sistemas de Información están ubicados en
escuelas de negocios. Todos los programas de sistemas de información
combinan cursos de computación y negocios. Una amplia variedad de
programas de Sistemas de Información existen bajo diversos nombres los
cuales usualmente reflejan la naturaleza del programa. Por ejemplo,
programas en Computer Information Systems usualmente tienen fuerte
enfoque tecnológico, y programas en Management Information Systems
pueden enfatizar aspectos de organización y comportamiento de los
sistemas de información. Los nombres de estos programas no siempre son
consistentes.
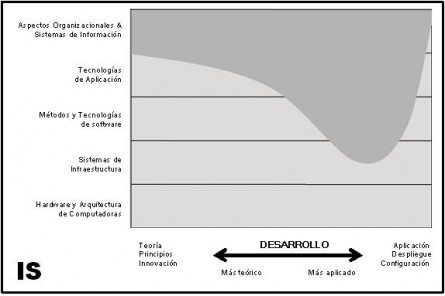
Information Technology (Tecnología de Información)
Tecnologías
de Información es una etiqueta que tiene dos significados. En un
sentido amplio, el término “tecnologías de información” es usualmente
empleado para referirse a toda la computación. En el ámbito académico,
se refiere a los programas de pregrado que prepara estudiantes para
satisfacer las necesidades tecnológicas de los negocios, gobierno,
sector salud, escuelas, y otros tipos de organizaciones.
En
la sección previa, dijimos que Sistemas de Información se enfoca en los
aspectos de “información” de la “tecnologías de información”.
Tecnología de Información es el complemento de tal perspectiva: su
énfasis es más en la tecnología en sí misma que en la información que
procesa. Tecnología de Información es una disciplina nueva y rápidamente
creciente la cual empezó como una respuesta muy básica a las
necesidades prácticas y cotidianas de los negocios y otras
organizaciones. Hoy en día, organizaciones de todo tipo dependen de las
tecnologías de información. La necesitan para tener sistemas apropiados.
Estos sistemas deben trabajar adecuadamente, deben ser seguros, y deben
ser mejorables, mantenibles, y reemplazables cuando sea necesario. Las
personas a lo largo de una organización requieren el soporte del staff
de tecnología de información que entienda los sistemas de computadoras y
su software, y que estén comprometidos a resolver cualquier problema
relacionado de las computadoras que podrían ocurrir. Los graduados de
programas de tecnología de información resuelven estas necesidades.
Los
programas en Tecnología de Información aparecen porque los programas en
las otras disciplinas de la computación no estaban produciendo una
adecuada oferta de graduados capaces de manejar estas reales
necesidades. Los programas de Tecnología de Información existen para
producir graduados que poseen la correcta combinación de conocimiento y
práctica, experiencia hands-on para tomar el cuidado tanto de la
infraestructura de tecnología de información de una organización como de
las personas que las utilizan. Los especialistas en Tecnología de
Información asumen la responsabilidad para seleccionar los productos de
hardware y software apropiados para una organización, integrando estos
productos con las necesidades organizacionales y su infraestructura, e
instalando, adecuando y manteniendo estas aplicaciones para los usuarios
de las computadoras de la organización. Ejemplos de estas
responsabilidades incluyen: la instalación de redes; administración y
seguridad de redes; el diseño de páginas web; el desarrollo de recursos
multimedia; la instalación de componentes de comunicación; la
supervisión de productos e-mail; y el planeamiento y administración del
ciclo de vida tecnológico por el cual la tecnología de una organización
es mantenida, mejorada, y reemplazada.
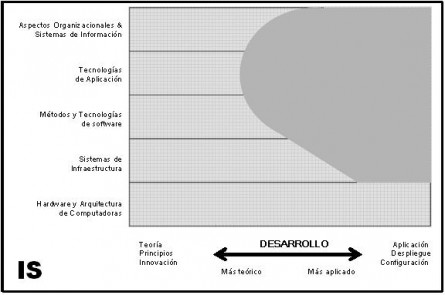
Software engineering (Ingeniería de Software)
La
Ingeniería de Software es la disciplina de desarrollo y mantenimiento
de sistemas software que se comportan de manera confiable y eficiente, y
que son factibles de desarrollar y mantener. Esto refleja sus orígenes
como se bosquejó en la sección 2.2.2. Sin embargo, más recientemente ha
evolucionado en respuesta a la creciente importancia del software en
aplicaciones de seguridad crítica y para el creciente impacto de grandes
y costosos sistemas software en un amplio rango de situaciones. La
Ingeniería de Software es diferente en su carácter de otras disciplinas
de Ingeniería, debido tanto a la naturaleza intangible del software y a
la naturaleza discontinua de la operación del software. Esta busca
integrar los principios de las matemáticas y las ciencias de la
computación con las prácticas de Ingeniería desarrollada para objetos
físicos tangibles. Los estudiantes interesados pueden esperar ver a la
Ingeniería de Software presentada en dos contextos:
Programas
en Ciencias de la Computación ofrecen uno o más cursos de Ingeniería de
Software como parte de su currículo en Ciencias de la Computación.
Algunos ofrecen una concentración de múltiples cursos de Ingeniería de
Software dentro de Ciencias de Computación.
Un cierto número de instituciones ofrecen un programa en pregrado en Ingeniería de Software.
Los
programas en Ciencias de Computación y en Ingeniería de Software tienen
muchos cursos en común. Los estudiantes de Ingeniería de Software
aprenden más acerca de confiabilidad y mantenimiento del software y se
enfocan más en técnicas para desarrollar y mantener software que es
correcto desde su concepción. Mientras los estudiantes de Ciencias de la
Computación probablemente hayan escuchado de la importancia de tales
técnicas, el conocimiento y experiencia ingenieril proporcionado en
programas de Ingeniería de Software va más allá de lo que los programas
de Ciencias de la Computación pueden proporcionar. Tal es la importancia
de esto que una de las recomendaciones del reporte de Ingeniería de
Software es que durante su programa de estudios, los estudiantes de
Ingeniería de Software deben participar en el desarrollo de software a
ser usado seriamente por otros. Los estudiantes de Ingeniería de
Software aprenden como asegurar las necesidades de los clientes y
desarrollan software usable que satisface estas necesidades. Conociendo
como proporcionar software genuinamente útil y usable es de máxima
importancia.
En
el campo laboral, el término “Ingeniero de Software” es un cargo
laboral. No hay una definición estándar para este término cuando se usa
como una descripción laboral. Su significado varía ampliamente entre
empleadores. Este puede ser un título equivalente a “programador de
computadoras” o un título para aquellos que administran un proyecto de
software grande, complejo y/o de seguridad crítica. El público no debe
confundir la disciplina de la Ingeniería de Software con el ambiguo uso
del término “Ingeniero de Software” al ser usado la publicidad de
ofertas de empleo y en cargos laborales.
Suscribirse a:
Comentarios (Atom)

